五、偏序集中极小元,极大元,最小元,最大元,上界,下界,上确界,下确界。
等价关系和偏序关系
重点:(1) 掌握等价关系和等价类的概念,
(2) ![]() 上的等价关系与集合
上的等价关系与集合 ![]() 的划分之间的联系,
的划分之间的联系,
(3) 掌握偏序关系的概念,
(4) 偏序集哈斯图的画法。
1、等价关系的定义。
若 ![]() 上关系
上关系 ![]() 满足自反,对称,传递,则称
满足自反,对称,传递,则称 ![]() 为
为 ![]() 上的等价关系。若
上的等价关系。若
![]() ,记
,记 ![]() 。
。
例1、(1) 集合
![]() 上的恒等关系,全域关系是等价关系。
上的恒等关系,全域关系是等价关系。
(2) 三角形的全等关系,三角形的相似关系是等价关系。
(3) 在一个班级里“年龄相等”的关系是等价关系。
例2、 ![]() ,
, ![]() (其中
(其中 ![]() 也就是
也就是 ![]() ,称模
,称模 ![]() 的同余关系),验证
的同余关系),验证
![]() 为
为 ![]() 上的等价关系。
上的等价关系。
证明:
![]() ,
,
显然, ![]() 满足自反,对称,传递,所以
满足自反,对称,传递,所以 ![]() 是等价关系。
是等价关系。
![]() 的关系图如下:
的关系图如下:
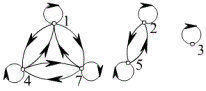
其中 ![]() ,
, ![]() 。
。
把模 ![]() 的同余关系推广,对正整数
的同余关系推广,对正整数 ![]() ,整数集
,整数集 ![]() 上模
上模 ![]() 的同余关系是等价关系:
的同余关系是等价关系: ![]()
事实上:(1)
![]() ,
, ![]() ,故
,故 ![]() ,
, ![]() 是自反的。
是自反的。
(2)
若 ![]() ,即
,即 ![]() ,则
,则 ![]() ,故
,故 ![]() ,
, ![]() 是对称的。
是对称的。
(3)
若 ![]() ,
, ![]() ,即
,即 ![]() ,
, ![]() ,因
,因 ![]() ,所以
,所以 ![]() ,故
,故 ![]() ,
, ![]() 是传递的。
是传递的。
由(1),(2),(3),
![]() 是等价关系。
是等价关系。
例3、设 ![]() 是
是 ![]() 上的自反关系,且当
上的自反关系,且当 ![]() ,
, ![]() 时,有
时,有 ![]() ,证明
,证明 ![]() 是等价关系。
是等价关系。
证明:已知 ![]() 是自反的,要证
是自反的,要证 ![]() 是等价关系,只要证
是等价关系,只要证 ![]() 是对称的和传递的即可。
是对称的和传递的即可。
若 ![]() ,由
,由 ![]() 及
及 ![]() (
( ![]() 是自反的),有
是自反的),有 ![]() ,所以
,所以 ![]() 是对称的。
是对称的。
若 ![]() ,
, ![]() ,由
,由 ![]() 的对称性,有
的对称性,有 ![]() ,又
,又 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() 是传递的。
是传递的。
由于 ![]() 是自反,对称,传递的,故
是自反,对称,传递的,故 ![]() 是等价关系。
是等价关系。
2、等价类。
(1)定义:设 ![]() 是非空集合
是非空集合 ![]() 上的等价关系,对
上的等价关系,对 ![]() ,记
,记
![]()
则称 ![]() 为
为 ![]() 关于
关于 ![]() 的等价类,简称
的等价类,简称 ![]() 的等价类,记
的等价类,记 ![]() 。
。
在例2中,有
![]()
![]()
![]() 。
。
(2) 性质。(证明略)
定理:
![]() 是非空集合
是非空集合 ![]() 上的等价关系,
上的等价关系, ![]() ,
,
(ⅰ) ![]() ,且
,且 ![]() ,
,
(ⅱ)
若 ![]() ,则
,则 ![]() ,
,
(ⅲ)
若 ![]() ,则
,则 ![]() ,
,
(ⅳ) ![]() 。
。
在例2中, ![]() ,
, ![]() ,
, ![]() 都是
都是 ![]() 的非空子集,
的非空子集, ![]() ,
, ![]() 或
或 ![]() (由
(由 ![]() 或
或 ![]() 决定),
决定), ![]() 。
。
3、商集。
定义:设 ![]() 为非空集合
为非空集合 ![]() 上的等价关系,以
上的等价关系,以 ![]() 的不交的等价类为元素的集合叫做
的不交的等价类为元素的集合叫做
![]() 在
在 ![]() 下的商集,记作
下的商集,记作 ![]() ,即
,即 ![]() 。
。
例如:在例2中, ![]() 。
。
例4、(1) 非空集合
![]() 上的恒等关系
上的恒等关系 ![]() 是等价关系,
是等价关系, ![]() ,
, ![]() ,所以商集
,所以商集 ![]() 。
。
(2)
非空集合 ![]() 上的全域关系
上的全域关系 ![]() 是等价关系,
是等价关系, ![]() ,
, ![]() ,所以商集
,所以商集 ![]() 。
。
例5、整数集 ![]() 上模
上模 ![]() 的等价关系
的等价关系 ![]()
其等价类是:
![]()
![]()
![]()
……
![]()
商集 ![]()
1、划分的定义。
![]() 是非空集合,
是非空集合, ![]() 是它的子集,满足:
是它的子集,满足:
(1) ![]()
(2) ![]()
则称 ![]() 为
为 ![]() 的一个划分,而
的一个划分,而 ![]() 称为这个划分的块。
称为这个划分的块。
例6、设 ![]() ,判断下列子集族是否
,判断下列子集族是否 ![]() 的划分。
的划分。
(1) ![]() ,
,
(2) ![]() ,
,
(3) ![]() ,
,
(4) ![]() ,
,
(5) ![]() 。
。
解:(1),(2),(3)不是
![]() 的划分,(4),(5)是
的划分,(4),(5)是
![]() 的划分。
的划分。
2、集合 ![]() 的一个划分确定
的一个划分确定 ![]() 的一个等价关系。
的一个等价关系。
比较某集合 ![]() 的划分与
的划分与 ![]() 的等价关系的商集的定义,可以发现,
的等价关系的商集的定义,可以发现,
![]() 上的一个划分
上的一个划分 ![]() 把
把 ![]() 分成若干划分块,若定义同一块中的元素有关系
分成若干划分块,若定义同一块中的元素有关系 ![]() ,可以证明
,可以证明 ![]() 是
是 ![]() 上的一个等价关系,称为划分
上的一个等价关系,称为划分 ![]() 诱导的等价关系,则这个划分的块就是等价关系的等价类,划分就是商集。
诱导的等价关系,则这个划分的块就是等价关系的等价类,划分就是商集。
如例6中的(4)的划分确定
![]() 上的一个等价关系
上的一个等价关系 ![]() 如下:
如下:
![]()
商集: ![]()
3、 ![]() 上的一个等价关系可确定
上的一个等价关系可确定 ![]() 的一个划分。
的一个划分。
若 ![]() 为
为 ![]() 上的等价关系,求出
上的等价关系,求出 ![]() 的所有不同等价类。由于这些等价类都是
的所有不同等价类。由于这些等价类都是
![]() 的子集,且不同等价类之间不交,所有等价类的并集就是
的子集,且不同等价类之间不交,所有等价类的并集就是 ![]() ,所有等价类的集合,即商集
,所有等价类的集合,即商集 ![]() ,就是
,就是 ![]() 的一个划分,称为由
的一个划分,称为由 ![]() 诱导的划分。
诱导的划分。
如例2中由 ![]() 诱导的划分,即
诱导的划分,即 ![]() 。
。
由以上可知,集合 ![]() 上的等价关系与集合
上的等价关系与集合 ![]() 的划分是一一对应的。
的划分是一一对应的。
例7、设 ![]() ,求出
,求出 ![]() 上的所有的等价关系。
上的所有的等价关系。
解:只需列出 ![]() 上所有的划分,并找出由它们确定的等价关系。
上所有的划分,并找出由它们确定的等价关系。
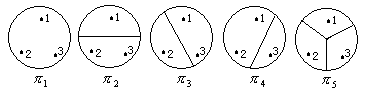
![]() 的不同划分只有以上五种,设对应于划分
的不同划分只有以上五种,设对应于划分
![]() 的等价关系为
的等价关系为 ![]() ,则有
,则有
![]()
![]()
![]()
![]()
![]()
例8、设 ![]() ,在
,在 ![]() 上定义等价关系
上定义等价关系 ![]() :
: ![]() ,
, ![]() 。
。
则由此等价关系诱导的划分中
(1) 共有几个划分块?
(2) 求其中最大的块。
(3) 求其中最小的块。
解:依题意得: ![]()
![]()
即第一元素与第二元素之差相等的有序对互相等价,将
![]() 中的元素按差划分。
中的元素按差划分。
差为 ![]() 的:
的: ![]() ,
,
差为 ![]() 的:
的: ![]()
差为 ![]() 的:
的: ![]()
差为 ![]() 的:
的: ![]()
差为 ![]() 的:
的: ![]()
(1)
共有 ![]() 个划分块。
个划分块。
(2)
最大的划分块为: ![]()
(3)
最小的划分块为: ![]() 和
和 ![]() 。
。
1、偏序关系的定义。
若 ![]() 上关系
上关系 ![]() 满足自反,反对称,传递,则称
满足自反,反对称,传递,则称 ![]() 为
为 ![]() 上的偏序关系,简称偏序,记作
上的偏序关系,简称偏序,记作 ![]() ,若
,若 ![]() ,记
,记 ![]() 。
。
![]() 也读作“
也读作“ ![]() 小于等于
小于等于 ![]() ”(并不是指数的大小)
”(并不是指数的大小)
集合 ![]() 与
与 ![]() 上的偏序关系
上的偏序关系 ![]() 一起叫做偏序集,记作
一起叫做偏序集,记作
![]() 。
。
例1、集合 ![]() 上的恒等关系,幂集
上的恒等关系,幂集 ![]() 上的包含关系,有理数集上的小于等于关系,正整数集上的整除关系都是偏序关系,分别记作偏序集
上的包含关系,有理数集上的小于等于关系,正整数集上的整除关系都是偏序关系,分别记作偏序集 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 。
。
2、偏序集中的两元素可比,盖住的定义。
设 ![]() 为偏序集,
为偏序集, ![]() ,若
,若 ![]() 或
或 ![]() 成立,则称
成立,则称 ![]() 是可比的,若
是可比的,若 ![]() (
( ![]() 且
且 ![]() ),且不存在
),且不存在 ![]() 使得
使得 ![]() ,则称
,则称 ![]() 盖住
盖住 ![]() 。
。
例2、 ![]() ,
, ![]() 为整除关系,
为整除关系, ![]() 为偏序集。
为偏序集。
![]() ,
, ![]() ,所以
,所以 ![]() 和
和 ![]() 都是可比的,但
都是可比的,但 ![]() 和
和 ![]() 就是不可比的,因
就是不可比的,因 ![]() 不能整除
不能整除 ![]() 且
且 ![]() 也不能整除
也不能整除 ![]() 。对于
。对于 ![]() 和
和 ![]() 来说,
来说, ![]() 且不存在
且不存在 ![]() 使
使 ![]() ,所以,
,所以, ![]() 盖住
盖住 ![]() ,同理,有
,同理,有 ![]() 盖住
盖住 ![]() ,但
,但 ![]() 不盖住
不盖住 ![]() ,因
,因 ![]() 。
。
3、全序集。
设 ![]() 为偏序集,若
为偏序集,若 ![]() ,
, ![]() 和
和 ![]() 都可比,则称
都可比,则称 ![]() 为
为 ![]() 上的全序关系,且称
上的全序关系,且称
![]() 为全序集。
为全序集。
例如: ![]() ,
, ![]() 是全序集,
是全序集, ![]() 不是全序集。
不是全序集。
1、哈斯图 ![]() 。
。
把偏序关系的关系图简化而得到哈斯图。步骤如下:
(1)
对偏序集 ![]() ,
, ![]() 中的每个元素用结点表示,结点的位置按它们在偏序中的次序由下向上排列 (即若
中的每个元素用结点表示,结点的位置按它们在偏序中的次序由下向上排列 (即若
![]() ,结点
,结点 ![]() 排在结点
排在结点 ![]() 的下方)。
的下方)。
(2)
若 ![]() 盖住
盖住 ![]() ,则在
,则在 ![]() 之间连一条线。
之间连一条线。
例3、画出 ![]() 的哈斯图,其中
的哈斯图,其中 ![]() 分别为
分别为
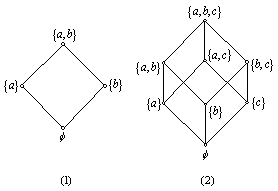
(1) ![]()
(2) ![]() 。
。
解:哈斯图如下:
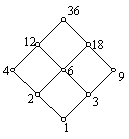
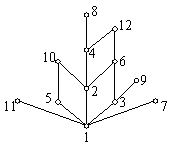
(1) (2)
例4、画出 ![]() 的哈斯图,其中
的哈斯图,其中 ![]() 分别为
分别为
(1) ![]()
(2) ![]() 。
。
解:(1) ![]()
(2) ![]()
哈斯图如下:
例5、 ![]() ,画出偏序集
,画出偏序集 ![]() 的哈斯图。
的哈斯图。
解:因 ![]() 为全序集 (任两元素均可比)
为全序集 (任两元素均可比)
其哈斯图为一直线
(右图): ![]()
例6、已知偏序集 ![]() 的哈斯图(右图),
的哈斯图(右图), 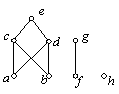
求集合 ![]() 的偏序关系
的偏序关系 ![]() 。
。
解:
![]()
![]()
五、偏序集中极小元,极大元,最小元,最大元,上界,下界,上确界,下确界。
1、极大、小元,最大、小元。
定义:设 ![]() 为偏序集,
为偏序集, ![]() ,
,
(1)
若 ![]() ,使得
,使得 ![]() 成立,则称
成立,则称 ![]() 是
是 ![]() 的最小元。
的最小元。
(2)
若 ![]() ,使得
,使得 ![]() 成立,则称
成立,则称 ![]() 是
是 ![]() 的最大元。
的最大元。
(3)
若 ![]() ,使得
,使得 ![]() 成立,则称
成立,则称 ![]() 是
是 ![]() 的极小元。
的极小元。
(4)
若 ![]() ,使得
,使得 ![]() 成立,则称
成立,则称 ![]() 是
是 ![]() 的极大元。
的极大元。
由定义知:
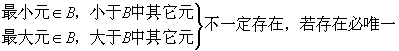
 。
。
2、上、下界,上、下确界。
定义:设 ![]() 为偏序集,
为偏序集, ![]() ,
,
(1)
若存在 ![]() ,使得
,使得 ![]() 成立,则称
成立,则称 ![]() 为
为 ![]() 的上界。
的上界。
(2)
若存在 ![]() ,使得
,使得 ![]() 成立,则称
成立,则称 ![]() 为
为 ![]() 的下界。
的下界。
(3)
令 ![]() ,称
,称 ![]() 中最小元为
中最小元为 ![]() 的上确界(最小上界)。
的上确界(最小上界)。
(4)
令 ![]() ,称
,称 ![]() 中最大元为
中最大元为 ![]() 的下确界(最大下界)。
的下确界(最大下界)。
由定义知:

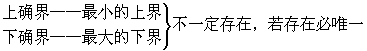
例7、 ![]() ,偏序集
,偏序集 ![]() ,
,
求 ![]() 的最大、小元,极大、小元,上、下界,上、下确界。
的最大、小元,极大、小元,上、下界,上、下确界。
(1) ![]()
(2) ![]() 。
。 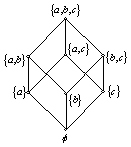
解:(1) ![]() 的最大元:无,最小元:无,
的最大元:无,最小元:无,
极大元: ![]() ,极小元:
,极小元: ![]() ,
,
上界: ![]() ,下界:
,下界: ![]() ,
,
上确界: ![]() ,下确界:
,下确界: ![]() 。
。
(2) ![]() 的最大元:
的最大元: ![]() ,最小元:无,
,最小元:无,
极大元: ![]() ,极小元:
,极小元: ![]()
上界: ![]() ,下界:
,下界: ![]()
上确界: ![]() ,下确界:
,下确界: ![]() 。
。
例8、设 ![]() ,问:
,问:
(1) ![]() 上可以定义多少种不同的二元关系?
上可以定义多少种不同的二元关系?
(2) 其中有多少种等价关系?
(3) 其中有多少种偏序关系?
(4) ![]() 和空关系
和空关系 ![]() 是等价关系吗?是偏序关系吗?
是等价关系吗?是偏序关系吗?
解:(1) 因
![]() ,
, ![]() ,
, ![]() 的不同子集共
的不同子集共 ![]() 个。也就是说
个。也就是说 ![]() 上可以定义
上可以定义 ![]() 种不同的二元关系。
种不同的二元关系。
(2)
因 ![]() ,不同的划分只有两种,即
,不同的划分只有两种,即 ![]() 和
和 ![]() ,所以只有
,所以只有 ![]() 种等价关系。
种等价关系。
(3)
因 ![]() 只有
只有 ![]() 个元素,不同的哈斯图只有以下三种:
个元素,不同的哈斯图只有以下三种:
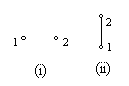
![]()
所以,有 ![]() 种偏序关系。
种偏序关系。
(4) ![]() 满足自反,对称和反对称,传递,所以
满足自反,对称和反对称,传递,所以
![]() 既是等价关系,又是偏序关系。
既是等价关系,又是偏序关系。
![]() 不满足自反性,所以既不是等价关系,又不是偏序关系。
不满足自反性,所以既不是等价关系,又不是偏序关系。