关系的闭包
重点：掌握关系的自反，对称，传递闭包的概念及求法。
1、定义：设 
是非空集合 
上的关系，
的自反闭包(对称闭包，传递闭包) 
也是
上关系，且满足：
(1)
是自反的(对称的，传递的)，
(2) 
，
(3)
对
上的任何包含
的自反关系(对称关系，传递关系) 
，都有 
。
由定义可知，
的闭包是包含
的且具有特殊关系(自反或对称或传递)的最小的关系。
2、记号。
——
的自反闭包，
——
的对称闭包，
——
的传递闭包。
1、利用以下公式。
(1) 
，
(2) 
，
(3) 
。
以上三个式子中，第三个式子 
，但对 
元集 ， 的不同的幂不超过
种，这时，可用 
，但对无穷集
就不一定是有限项了。
2、利用关系图。
(1)
的关系图：检查
的关系图，在没有环的结点上加上环，其它不变。
(2)
的关系图：检查
的关系图，把单向边改为双向边，其它不变。
(3)
的关系图，检查
的关系图，对每个结点 
，分别找出可以到达的终点 
，若
到
没有有向边，则添加一条有向边，直到添加完毕。
3、利用关系矩阵。
注意到以上公式，如 ，转换成关系矩阵，即 
( 
表示主对角线为1，其余为0的矩阵)，其中的“
”表示矩阵对应元素的逻辑加。同样，可得 
( 
为 
的转置)， 
。
例1、设 
，求 
。
[解法一]
(参考第二节例3)
[解法二]先画出
的关系图，再画出 的关系图。
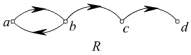
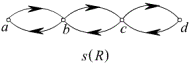
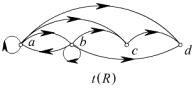
[解法三]利用关系矩阵(略)。