根树及其应用
重点：1、有向树及根树的定义，
2、家族树，有序树， 
元树的概念，
3、最优 
元树的概念及哈夫曼 
算法。
1、有向树：一个有向图 
，若略去有向边的方向所得的无向图为一棵无向树，则称
为有向树。
2、根树：一棵非平凡的有向树，如果有一个顶点的入度为 
，其余顶点的入度均为 
，则称此有向树为根树。入度为
的顶称为树根； 入度为1、出度为0的顶点称为树叶；入度为1、出度大于0的顶点称为内点，内点和树根统称为分支点。
注意：根树的画法可以是任意的，但常将根画在最上方，这时，有向边的方向均指向下方，故可略去其方向。
例1、
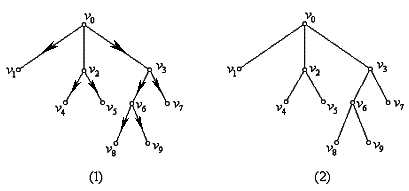
根树(1)可画成(2)，其中，
…………树根
， 
， 
， 
， 
， 
…………树叶
， 
， 
…………内点
3、树高。
的层数——从树根到顶点 
的通路长度，记 
。
树高——树中顶点的最大层数，记 
。
如例1中，
为
层， 
在第
层上， 
在第
层上， 
在第 
层上，树高为
。
4、家族树。
一棵根树可以看成一棵家族树。
(1) 若顶点 
邻接到顶点 
，则称
为
的儿子，
为
的父亲，
(2) 若 
同为
的儿子，则称
为兄弟，
(3) 若 
，而
可达 
，则称
为
的祖先，
为
的后代。
5、根子树。
树 
的根子树——
的非树根的顶点
及其后代导出的子图。
例2、
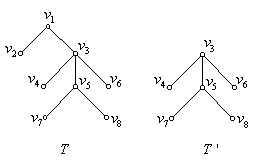
上图的根树
中， 
为兄弟，它们都是
的儿子，而
又有儿子 
，
有儿子 
，
为
的祖先，
为
的后代，……。
是
的根子树。
1、有序树——每一层上都规定次序的根树。
次序可排在顶点处，也可排在边上，一般从左到右。
2、 
元树——每个分支点至多有
个儿子的根树。
元正则树——每个分支点恰有
个儿子的根树。
元有序树——
元树，且是有序树。
元有序正则树——
元正则树，且是有序树。
元完全正则树——
元正则树，且所有树叶的层数相同 (等于树高)。
元有序完全正则树——
元正则完全树，且是有序树。
注意：
元有序正则树是最重要的一种
元树。
例3、
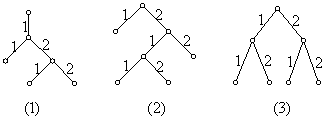
上图中，(1)为
元有序树，(2)为
元有序正则树，(3)为
元有序完全正则树。
3、最优
元树。
(1)定义：设
元树
有 
片树叶，分别带权为 
( 
为实数， 
)，称 
为
的权，其中 
为带权
的树叶 
的层数，在所有的带权
的
元树中，带权最小的
元树称为最优 
元树。
例4、
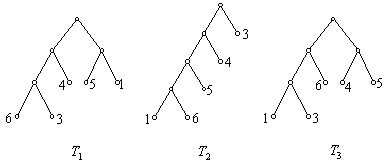
上图中的 
都是带权 
的
元树，求 
， 
， 
。
解： 
，
，
。
显然， 
，但还不能判定 
是最优
元树。
(2) 求最优
元树的算法。
算法：
给定实数 
(
片树叶的权)，且 
，
连接 
为权的两片树叶，得一分支点，其权为 
，
在 
中选出两个最小的权，连接它们对应的顶点 (不一定都是树叶)，得分支点及所带的权。
重复
，直到形成 
个分支点，
片树叶为止。
例5、求带权
的最优
元树
及 
。
解：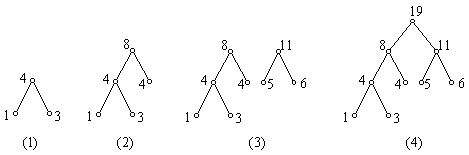
上图(1)，(2)，(3)，(4)即求最优
元树的过程，其中(4)为最优
元树。
，
其实
等于
的各分支点的权之和 (思考：为什么？)，即
，
比较例4，例5知，例4的
也是带权为
的最优
元树，因为
也是 
，可见，最优树是不唯一的，但
算法得到的树一定是最优树。
例6、(1) 求带权为 
的最优
元树
，
(2) 求
，
(3) 求
的高度
，
(4) 求
的树叶有多少？
(5) 求
的
度顶点，
度顶点， 
度顶点各有多少？
解：(1)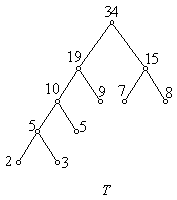 
(2) 
，
(3) 
，
(4)
的树叶有 
片，
(5)
的
度顶点
个 (即树根)，
度顶点
个 (即内点)，
度顶点
个。
4、求最佳前缀码。
最优
元树的用途之一是求最佳前缀码。
在通讯中，我们常用
和
的符号串作为英文字母的传送信息， 
个英文字母被使用的频率往往是不同的。为了使整个信息的长度尽可能短，自然希望用较短的符号串去表示使用频率高的英文字母，用较长的符号串表示使用频率低的英文字母。为了使编码在使用中既快速又准确，可以用求最优
元树的
算法解决这个问题。