一、两命题公式间的等值关系
二、重要等值式
三、等值演算
等值演算
重点：(1) 掌握两公式等值的定义。
(2) 掌握24个重要等值式，并能利用其进行等值演算。
1、定义：设 
为两命题公式，若等价式 
是重言式，则称 
与 
是等值的，记作 
。
2、判定。
判断两公式
是否等值，即判断
是否重言式，可用真值表的办法，看 的真值表的最后一列是否全为1，或者看
真值表中的值是否完全相同。
例1、判断
两公式是否等值。
(1) 
， 
(2) 
， 
解：(1) 作真值表如下：
|
表1
(2) 作真值表如下：
|
表2
以上表1中的第三列与最后一列不完全相同，所以 不等值；
以上表2中的第二列与最后一列完全相同，所以 
。
1、交换律 
， 
2、结合律 
， 
3、分配律 
，
4、德·摩根律 
， 
5、等幂律 
， 
6、吸收律 
， 
7、零律 
， 
8、同一律 
， 
9、互否律 
(排中律)， 
(矛盾律)
10、双重否定律 
11、蕴涵等值式 
12、等价等值式 
13、假言易位 
14、等价否定等值式 
15、归谬论 
以上15组共24条重要等值式，在等值演算中经常要用到，应该记住它们，并能熟练运用。其中 
表示任意的命题公式。以上每条都可用真值表检验，如例1.(2)验证了第12条。
置换定理：如果
，则 
。
根据置换定理及24条等值式就可进行等值演算。
例2、验证下列等值式。
(1) 
(2) 
(3) 
解：(1) 
蕴涵等值式
蕴涵等值式
结合律
德·摩根律
蕴涵等值式
(2) 
交换律
分配律
排中律
同一律
(3) 
分配律
矛盾律
同一律
德·摩根律
结合律
排中律
零律
由以上例子，我们可以考虑这个问题，能否利用等值式来化简，或判断公式的类型(重言，矛盾，可满足)。答案是肯定的，如例2.(2)中，左端的公式较复杂，而右端的公式很简单，由右式易知，111(即
)和011是此公式的成真赋值，而其余的均为成假赋值，从而此公式为可满足式。同理，例2.(1)中，110是成假赋值，其余均为成真赋值，此公式也是可满足式，例2.(3)中，左端的公式为重言式。
到现在为止，判断一个公式是否重言式，矛盾式，可满足式，或者判断两个命题公式是否等值。有两种方法，即真值表法和等值演算法。
例3、用两种方法证明： 
。
[证法一]用真值表法
|
由最后两列真值完全相同，即
[证法二]用等值式法
蕴涵等值式
双重否定律
交换律
结合律
吸收律
例4、将下图所示的逻辑电路简化
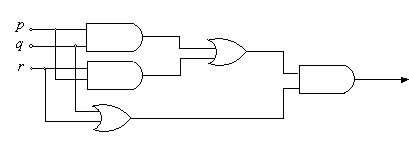
解：将上述逻辑电路写成命题公式
利用等值式将公式化简
原命题公式
分配律
结合律
等幂律
所以，该电路可简化为下图
